З непозиционной єгипетської системою числення, яка вживалася в Стародавньому Єгипті, нас наочно знайомлять деякі збереглися папіруси. Приклади задач та їх рішення в них настільки цікаві, що залишається тільки шкодувати, що їх так мало.
З них видно, що математика і єгипетська система числення були тісно пов’язані з господарськими потребами і практичним застосуванням. Кожен рік після розливу Нілу доводилося відновлювати будови, заново межевать земельні наділи, розраховуючи площу та межі, вести облік врожаю, календар.
Що таке позиційна і непозиционная системи счислений?
Відповідь криється в самій назві. Якщо позиція цифри впливає на результат обчислень, перед нами позиційна система чисел, якщо немає – непозиционная.
Якщо ми пишемо 12 – це дванадцять, а з тими ж цифрами 21 – це двадцять один. По єгипетській системі числення: щоб написати 12, знадобиться використовувати два рази символ одиниці і один раз символ десятки, а 21 буде виглядати як один знак одиниці і два знаки десятки, тобто всього треба написати три знака.
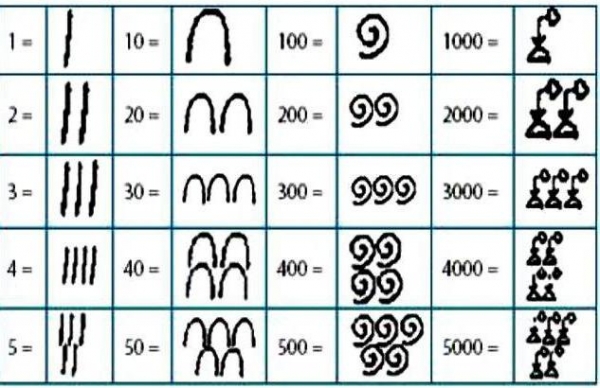
До непозиционным відносяться: знайома нам римська система, в якій цифри позначалися римськими літерами, слов’янська система, де кожна буква позначала якусь цифру або число. Римська система справлявся зі своїми функціями в Західній Європі до 16 століття.
Використовувана нами система числення в сучасному житті – позиційна десяткова система.
Непозиционные системи добре підходили для виконання простих арифметичних дій, так як складні обчислення припускали громіздкі записи, що не заважало в Стародавньому Єгипті успішному розвитку алгебри й геометрії.
Як вважали єгиптяни?
Що це таке – єгипетська система числення? Щоб написати яке-небудь число, використовували ієрогліфи, що позначали певні числа, сума яких дорівнювала потрібного значення.
Спеціальні позначення були для чисел 1, 10, 100, 1000, 10000, 100000, 1000000. При написанні потрібного числа кожне позначення використовувалося до 9 разів. Запис в єгипетській системі числення йшла за зростанням: спочатку одиниці, потім десятки, сотні і так далі.
Причому писали, як правило, справа наліво, але можна було і зліва направо, сума від цього не змінювалася. Використовувалося і вертикальне написання, але тоді відлік йшов зверху вниз.
Використовувалося два способи написання:
Екскурс в історію
Історія єгипетської системи числення виникла в глибоку давнину, перші рукописи з цифрами відносяться до другого тисячоліття до нашої ери. Грошей тоді не було, тому система використовувалася як для неймовірних по складності і величі математичних задач, так і для вирішення щоденних побутових питань.
Адже знання математики використовувалося і при межуванні земель, і при побудові календарів, карт в астрономії, мореплаванні, при будівництві палаців, каналів і військових укріплень.
Єгипетська непозиционная система числення застосовувалася до 10 століття нашої ери.
Вона мала і містичне значення, таємницю якого забрали з собою жерці, але частково відкрив світу Піфагор. У нього є праці, в яких він описує символічні значення, які надаються цифровим ієрогліфам, написані ним після перебування в Єгипті. Тому відносять їх опис до єгипетській системі числення.
Збереглося лише кілька папірусів тих часів, за якими можна зрозуміти, що рівень математики був високий. Достовірно відомо, що греки вивчали давньоєгипетську математику. Одним з таємних знань є єгипетська непозиционная система числення.
Папірус Ахмеса
Папірус Ахмеса датується 1650 р. до н. е., містить 84 математичні задачі. Він був знайдений в Фівах, зберігається в Британському музеї.
Всі завдання в папірусі розглянуті на конкретних прикладах єгипетської системи числення. У них показуються приклади розрахунків з дробами, з цілими числами, розподілом і множенням.
Дані розрахунки для знаходження площ геометричних фігур: чотирикутника, кола, трикутника.
Відомості з папірусу доводять, що єгипетські математики вміли добувати корінь, складати арифметичну і геометричну прогресію, рівняння з невідомими.
Аликвотные дробу
Цікаво, що в розрахунках використовувалися тільки аликвотные дроби, у яких чисельник дорівнює одиниці і позначався таким знаком, а під ним писалися значення знаменника, а всі інші дроби для розрахунків спочатку потрібно було розкласти до аліквотних. Але використовувались і мали спеціальне позначення дробу 2/3 і 3/4.
Для приведення звичайних дробів у стан аліквотних по єгипетській системі числення потрібно було потрудитися:
4/5 = 16/20 = 10/20 + 5/20 + 1/20 = 1/2+1/4 + 1/20
2/5 = 1/5 + 1/5, 2/7 = 1/4 + 1/28
3/7 = 12/28 = 24/56 = 14/56+7/56+3/56 = 1/4+1/8+1/18+1/56.
Складалися дробу сучасним способом: приведенням до спільного знаменника, для багатьох значень були численні готові таблиці.
Множення
Єгиптяни дізнавалися потрібний результат, не знаючи таблиці множення, але використовуючи знання про те, що, якщо один множник збільшити в два рази, а інший зменшити, то результат не зміниться:
32*13=16*26=8*52=4*104=2*208=1*416
Цікаво, що цей спосіб множення був відомий на Русі, і вважалося, що він прийшов з Давнього Єгипту, а в Європі його називали руським.
Папірус Голенищева
Завдяки старанням вченого-єгиптолога В. С. Голенищева, в Москві зберігається папірус ще на 200 років древнє папірусу писаря Ахмеса. Вчений купив його під час своєї роботи в Фівах.
Він був написаний иератическим способом, курсивом, в ньому розглядається 25 завдань, дано їх опис по єгипетській системі числення і вирішення. Його довжина понад 5 м при ширині 7 див. До цих завдань немає жодних коментарів, як і в попередньому папірусі, є тільки математичні розрахунки.
Він показує, що єгиптяни вміли обчислювати площі трикутника, трапеції, прямокутники, кола, а також обсяги піраміди, призми, паралелепіпеда, циліндра і усіченої піраміди з великою точністю, а багато формули повністю збігаються з сучасними.
При єгипетській системі числення було обчислено число «пі» 3,16, що майже відповідало сучасному значенню 3,14, хоча в ті часи повсюдно на Сході використовувалося значення, рівне 3.
Усі речі – сутність числа
Вважається, що Піфагор прожив в Єгипті 22 роки, глибоко вивчаючи геометрію, філософію, містику цифр. Ті відкриття, які пізніше робила Піфагорійська школа, цілком могли бути здійснені ще в Стародавньому Єгипті.
Тому вважається, що праці Піфагора про містику цифр, які він написав пізніше, засновані на таємних знаннях, отриманих ним від єгипетських жерців. Вони не брали на навчання іноземців, потрапив він до них з високою протекції, після співбесіди з головним жерцем, який визнав його гідним бути присвяченим у таємниці.
Числа були живими істотами, що відображають властивості простору, музики, енергії. Все можна висловити через математику, описавши формулами видимі явища передбачити невидимі, спираючись на логіку та математичні закономірності.
Висота, ширина підстави, кут нахилу піраміди Хеопса в Єгипті відповідають математичного правилом побудови піраміди Піфагора, що також підтверджує взаємозв’язок зроблених ним відкриттів і знань, отриманих від давньоєгипетських жерців, які використовували єгипетську систему числення.
Працюючи з цифрами, стародавні мислителі не тільки розуміли суть речей, але і могли впливати на них.
Вивчаючи математику Стародавнього Єгипту, що використовує єгипетську систему числення, можна лише захоплюватися тим, як багато було відкрито людям за тисячі років до нашої ери.
