Тим, хто цікавиться історією теореми Піфагора, яку вивчають у шкільній програмі, буде також цікавий такий факт, як публікація в 1940 році книги з трьохсот сімдесятьма доказами цієї, здавалося б, простий теореми. Але вона інтригувала уми багатьох математиків і філософів різних епох. У книзі рекордів Гіннеса вона зафіксована, як теорема з максимальною кількістю доказів.
Історія теореми Піфагора
Пов’язана з ім’ям Піфагора, теорема була відома задовго до народження великого філософа. Так, в Єгипті, при будівництві споруд, враховувалося співвідношення сторін прямокутного трикутника п’ять тисячоліть тому. У вавилонських текстах згадується про все те ж співвідношення сторін прямокутного трикутника за 1200 років до народження Піфагора.

Виникає питання, чому тоді свідчить історія виникнення теореми Піфагора належить йому? Відповідь може бути тільки один – він довів співвідношення сторін в трикутнику. Він зробив те, що століття тому не робили ті, хто просто користувався співвідношенням сторін і гіпотенузи, встановленим досвідченим шляхом.
З життя Піфагора
Майбутній великий учений, математик, філософ, народився на острові Самосі в 570 році до нашої ери. Історичні документи зберегли відомості про батька Піфагора, який був різьбярем по дорогоцінному камінню, а от про матір відомостей немає. Про народжену хлопчика говорили, що це неабиякий дитина, виявив з дитячого віку пристрасть до музики і поезії. До вчителів юного Піфагора історики відносять Гермодаманта і Ферекід Сиросского. Перший ввів хлопчика в світ муз, а другий, будучи філософом і засновником італійської школи філософії, спрямував погляд юнака до логосу.
У 22 роки від роду (548 р. до н. е..) Піфагор вирушив у Навкратис для вивчення мови і релігії єгиптян. Далі його шлях лежав в Мемфіс, де завдяки жерцям, пройшовши через їхні хитромудрі випробування, він збагнув єгипетську геометрію, яка, можливо наштовхнула допитливого юнака на доказ теореми Піфагора. Історія надалі припише теоремі саме це ім’я.

В полоні царя Вавилона
По дорозі додому в Елладу, Піфагор потрапляє в полон царя Вавилона. Але знаходження в полоні принесло користь допитливому розуму початківця математика, йому було чому повчитися. Адже в ті роки математика у Вавилоні була більш розвинутою, ніж у Єгипті. Дванадцять років він провів за вивченням математики, геометрії та магії. І, можливо, саме вавилонська геометрія причетна до доведення співвідношення сторін трикутника та історії відкриття теореми. У Піфагора було для цього достатньо отриманих знань і часу. Але, що це сталося у Вавилоні, документального підтвердження або спростування того немає.
У 530 р. до н. е. Піфагор біжить з полону на батьківщину, де живе при дворі тирана Полікрата в статусі полураба. Таке життя Піфагора не влаштовує, і він видаляється в печери Самоса, а потім відправляється на південь Італії, де в той час розташовувалася грецька колонія Кротон.
Таємний чернечий орден
На базі цієї колонії Піфагор організував таємний чернечий орден, який являв собою релігійний союз і наукове товариство одночасно. Це товариство мало свій статут, в якому йшлося про дотримання особливого способу життя.

Піфагор стверджував, щоб зрозуміти Бога, людина повинна пізнати такі науки як алгебра і геометрія, знати астрономію і розуміти музику. Дослідницька робота зводилася до пізнання містичної боку чисел і філософії. Слід зазначити, що проповедованные в той час Піфагором принципи, мають сенс в наслідуванні і в даний час.
Багато відкриттів, які робили учні Піфагора, приписувалися йому. Тим не менш, якщо говорити коротко, історія створення теореми Піфагора древніми істориками і біографами того часу, пов’язується безпосередньо з ім’ям цього філософа, мислителя і математика.
Вчення Піфагора
Можливо, на думку про зв’язок теореми з ім’ям Піфагора наштовхнуло істориків вислів великого грека, що в горезвісному трикутнику з його катетами і гіпотенузою зашифровані всі явища нашого життя. А цей трикутник є “ключем” до вирішення всіх виникаючих проблем. Великий філософ говорив, що слід побачити трикутник, тоді можна вважати, що завдання на дві третини вирішена.

Про своєму вченні Піфагор розповідав тільки своїм учням усно, не роблячи ніяких записів, тримаючи його в таємниці. На превеликий жаль, вчення видатного філософа не збереглося до наших днів. Що-то з нього просочилося, але не можна сказати скільки істинного, а скільки помилкового в тому, що стало відомо. Навіть з історією теореми Піфагора не всі безперечно. Історики математики сумніваються в авторстві Піфагора, на їхню думку теоремою користувалися за багато століть до його народження.
Теорема Піфагора
Може здатися дивним, але історичних фактів доведення теореми самим Піфагором немає — ні в архівах, ні в яких інших джерелах. У сучасній версії вважається, що воно належить не кому іншому, як самому Евклідом.
Є докази одного з найбільших істориків математики Моріца Кантора, виявив на папірусі, що зберігається в Берлінському музеї, записане єгиптянами приблизно в 2300 році до н. е. рівність, яка наголошувала: 32 + 42 = 52.
Коротко з історії теореми Піфагора
Формулювання теореми з евклідових “Почав”, що в перекладі звучить як і в сучасній інтерпретації. Нового в її прочитанні немає: квадрат противолежащей сторони прямому куту, дорівнює сумі квадратів сторін, прилеглих до прямого кута. Про те, що теорема користувалися стародавні цивілізації Індії та Китаю підтверджує трактаті “Чжоу — бі суань цзинь”. Він містить відомості про єгипетському трикутнику, в якому описано співвідношення сторін 3:4:5.

Не менш цікава ще одна китайська математична книга «Чу-пий», в якій також згадується про піфагоровому трикутнику з поясненнями і малюнками, що збігаються з кресленнями індуської геометрії Басхары. Про самому трикутнику в книзі написано, що якщо прямий кут можна розкласти на складові частини, тоді лінія, яка з’єднує кінці сторін, буде дорівнює п’яти, якщо основа дорівнює трьом, а висота дорівнює чотирьом.
Індійський трактат “Сульва сутра”, що відноситься приблизно до VII-V століть до н. е.., розповідає про побудову прямого кута за допомогою єгипетського трикутника.
Доказ теореми
У середні століття учні вважали доказ теореми занадто важким справою. Слабкі учні заучували теореми напам’ять, без розуміння сенсу докази. У зв’язку з цим вони отримали прізвисько “віслюки”, тому що теорема Піфагора була для них непереборною перешкодою, як для осла міст. У середні століття учні придумали жартівливий вірш на предмет цієї теореми.
Щоб довести теорему Піфагора найлегшим шляхом, слід просто виміряти його боку, не використовуючи в доказі поняття про площі. Довжина сторони, противолежащая прямому куту – це c, а прилеглі до нього a і b, в результаті отримуємо рівняння: a2 + b2 = c2. Дане твердження, як говорилося вище, перевіряється шляхом вимірювання довжин сторін прямокутного трикутника.
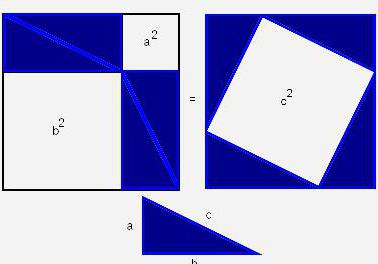
Якщо почати доказ теореми з розгляду площі прямокутників, побудованих на сторонах трикутника, можна визначити площу фігури. Вона буде дорівнює площі квадрата зі стороною (a+b), а з іншого боку, сумі площ чотирьох трикутників і внутрішнього квадрата.
(a + b)2 = 4 x ab/2 + c2;
a2 + 2ab + b2;
c2 = a2 + b2, що і було потрібно довести.
Практичне значення теореми Піфагора полягає в тому, що з її допомогою можна знайти довжини відрізків, не вимірюючи їх. При будівництві споруд розраховуються відстані, розміщення опор і балок, визначаються центри тяжкості. Застосовується теорема Піфагора і у всіх сучасних технологіях. Не забули про теорему і при створенні кіно в 3D-6D-вимірах, де крім звичних нам 3-х величин: висоти, довжини, ширини – враховуються час, запах і смак. Як пов’язані з теоремою смаки і запахи – запитаєте ви? Все дуже просто – при показі фільму потрібно розрахувати, куди і які запахи і смаки направляти в глядацькому залі.
Чи То ще буде. Безмежний простір для відкриття та створення нових технологій чекає допитливі розуми.