Теорія імовірностей – розділ математики, який готовий заплутати самих математиків. На відміну від інших, точних і непорушних догм цієї науки, дана область кишить дивацтвами і неточностями. В цей розділ зовсім недавно додали так сказати новий параграф – парадокс Монті Холла. Це, загалом, завдання, але вирішується вона зовсім не так, як звичні нам шкільні або університетські.
Історія походження
Над парадоксом Монті Холла люди ламають свої голови, починаючи з далекого 1975 року. Але почати варто з 1963. Саме тоді на екрани вийшло телешоу під назвою let’s make a deal, що перекладається як “Давайте укладемо угоду”. Його ведучим став ніхто інший як Монті Хол, який підкидав глядачам часом нерозв’язні завдання. Однією з найбільш яскравих стала та, яку він представив у 1975 році. Завдання стала частиною математичної теорії ймовірності і парадоксів, які укладаються в її рамки. Варто також зазначити, що дане явище стало причиною сильних дискусій і жорсткої критики з боку вчених. Парадокс Монті Холла був опублікований в журналі Parade в 1990 році, і з тих пір став ще більш обговорюваним і спірним питанням всіх часів і народів. Ну а тепер переходимо безпосередньо до його формулювання та трактування.
Формулювання проблеми
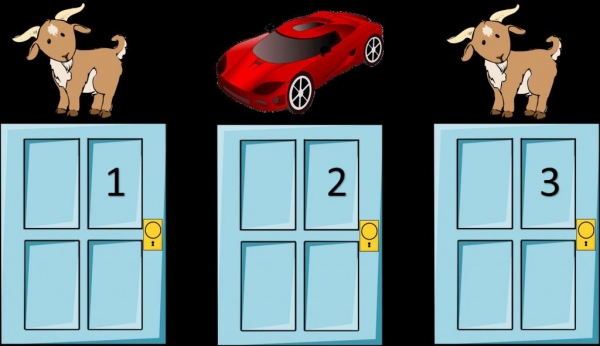
Існує безліч трактувань даного парадоксу, але ми вирішили представити вам класичну, яка була показана в самій програмі. Отже, перед вами три двері. За однією з них знаходиться автомобіль, за двома іншими по одній козі. Ведучий пропонує вам вибрати одну з дверей, і, припустимо, ви зупиняєтеся на номері-1. Поки що ви не знаєте, що за цієї самої першої дверима, так як вам відкривають третю, і показують, що за нею коза. Отже, ви поки що не програли, адже ви не вибрали ті двері, яка приховує програшний варіант. Отже, ваші шанси на отримання машини зростають.

Але тут ведучий пропонує вам змінити рішення. Перед вами вже двоє дверей, за однією коза, за інший бажаний приз. Саме в цьому і полягає суть проблеми. Здається, що яку б двері з двох ви не вибрали, шанси будуть 50 на 50. Але насправді, якщо ви поміняєте рішення, вірогідність того, що ви переможете, стане більше. Як так?
Пояснення парадоксу Монті Холла
Перший вибір, який ви робите в цій грі – випадковий. Ви ніяк не можете навіть віддалено здогадуватися, за якою з трьох дверей захований приз, тому рандомно вказуєте на першу-ліпшу. Ведучий ж в свою чергу знає, де що знаходиться. У нього є двері з призом, двері, на яку ви вказали, і третя без призу, яку він вам і відкриває в якості першої підказки. Друга ж підказка криється в самому його пропозиції змінити вибір.
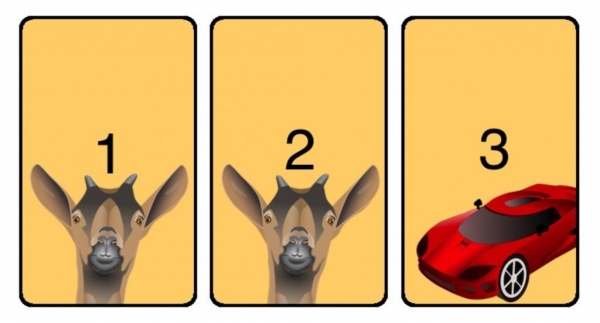
Тепер ви вже будете вибирати не навмання одну з трьох, а зможете навіть змінити своє рішення, щоб отримати бажаний приз. Саме пропозицію ведучого дає людині віру в те, що автомобіль знаходиться дійсно не за тими дверима, яку він обрав, а за інший. В цьому і полягає вся суть парадоксу, так як, по суті, вибирати (хоч вже з двох, а не трьох) все одно доводиться навмання, але шанси на перемогу зростають. Як показує статистика, з 30-ти гравців, які змінили своє рішення, машину виграли 18. А це 60%. А з тих же 30-ти осіб, які рішення не змінили – всього 11, тобто 36%.
Трактування в цифрах
Тепер дамо парадоксу Монті Холла більш точне визначення. Перший вибір гравця розбиває двері на дві групи. Ймовірність того, що приз розташований за дверима, яку ви обрали, становить 1/3, а за тими дверима, що залишилися 2/3. Ведучий далі відкриває одну з дверей другої групи. Таким чином він переносить всю решту ймовірність, 2/3, на одну двері, яку ви не вибрали і яку він не відкривав. Логічно, що після таких розрахунків вигідніше буде змінити своє рішення. Але при цьому важливо пам’ятати, що шанс програти все-таки є. Часом провідні лукавлять, так як ви спочатку можете тицьнути на правильну, призову двері, а потім від неї добровільно відмовитися.

Всі ми звикли до того, що математика, як точна наука, йде рука об руку зі здоровим глуздом. Тут справа роблять цифри, а не слова, точні формули, а не туманні міркування, координати, а не відносні дані. Але її новий розділ під назвою теорія ймовірностей підірвав увесь звичний шаблон. Завдання з цієї області, як нам здається, не вкладаються в рамки здорового глузду і повністю суперечать всім формул і обчислень. Пропонуємо нижче ознайомитися з іншими парадоксами теорії ймовірності, які мають щось спільне з тим, який був описаний вище.
Парадокс хлопчика і дівчинки
Задачка, на перший погляд, абсурдна, але вона суворо підпорядковується математичної формули і має два варіанти рішення. Отже, у якогось чоловіка двоє дітей. Один з них напевно хлопчик. Яка ймовірність того, що виявиться хлопчиком другий?
Варіант 1. Ми розглядаємо всі комбінації двох дітей в сім’ї:
- Дівчинка/дівчина.
- Дівчинка/хлопчик.
- Хлопчик/дівчинка.
- Хлопчик/хлопчик.
Перша комбінації нам очевидно не підходить, тому, виходячи з трьох останніх, ми отримуємо ймовірність 1/3 того, що другою дитиною виявиться маленький чоловік.

Варіант 2. Якщо ж уявити собі такий випадок на практиці, відкинувши дробу і формули, то, виходячи з того факту, що на Землі є лише дві статі, ймовірність того, що другою дитиною буде хлопчик, становить 1/2.
Парадокс сплячої красуні
Цей досвід показує нам, як хвацько можна маніпулювати статистикою. Отже, “сплячої красуні” вколюють снодійне і кидають монетку. Якщо випадає орел, то її будять і експеримент припиняється. Якщо ж випадає решка, то її будять, відразу роблячи другий укол, і вона забуває про те, що прокидалася, а після цього знову пробуджують лише на другий день. Після повного пробудження “красуні” невідомо, в який день вона відкрила очі, або яка ймовірність того, що монета впала решкою. По першому варіанту рішення ймовірність випадання решки (або орла) становить 1/2. Суть другого варіанта полягає в тому, що, якщо проводити експеримент 1000 разів, то у випадку з орлом “красуню” будуть будити 500 разів, а з рідкісною – 1000. Тепер уже ймовірність випадання решки становить 2/3.









