Ідея генетичних алгоритмів (ГА) з’явилася досить давно (1950-1975 рр..), але по-справжньому об’єктом вивчення вони стали лише в останні десятиліття. Першовідкривачем у цій області визнано вважати Д. Холланда, який запозичив багато з генетики та адаптував під обчислювальні машини. ГА широко використовуються в системах штучного інтелекту, нейронних мережах і задачах оптимізації.
Еволюційний пошук
Моделі генетичних алгоритмів були створені на базі еволюції в живій природі і методи рандомного пошуку. При цьому випадковий пошук є реалізацією найбільш простий функції еволюції – випадкових мутацій і подальшого відбору.
Еволюційний пошук з математичної точки зору означає не що інше, як перетворення наявного кінцевого безлічі рішень в нове. Функція, що відповідає за цей процес, і є генетичний пошук. Головною відмінністю такого алгоритму від випадкового пошуку є активне використання накопиченої в ході ітерацій (повторень) інформації.
Навіщо потрібні генетичні алгоритми
ГА переслідують наступні цілі:
- пояснити адаптаційні механізми як в природному середовищі, так і в інтелектуально-дослідної (штучної) системі;
- моделювання еволюційних функцій та їх застосування для ефективного пошуку рішень різних задач, головним чином оптимізаційних.
На даний момент суттю генетичних алгоритмів та їх модифікованих версій можна назвати пошук ефективних рішень з урахуванням якості результату. Іншими словами, пошук найкращого балансу між продуктивністю і точністю. Відбувається це за рахунок відомої всім парадигми «виживання найбільш пристосованою особини» в невизначених і нечітких умовах.
Особливості ГА
Перерахуємо головні відмінності ГА від більшості інших методів пошуку оптимального рішення.
- робота з закодованими певним чином параметрами задачі, а не безпосередньо з ними;
- пошук рішення відбувається не шляхом уточнення початкового наближення, а в безлічі можливих рішень;
- використання тільки цільової функції, не вдаючись до її похідних і модифікаціям;
- застосування імовірнісного підходу до аналізу, замість строго детермінованого.
Критерії роботи
Генетичні алгоритми проводять розрахунки виходячи з двох умов:
При виконанні одного з цих умов генетичний алгоритм перестане виконувати подальші ітерації. Крім цього, використання ГА різних областей простору рішень дозволяє їм куди краще знаходити нові рішення, які мають відповідні значення цільової функції.
Базова термінологія
Зважаючи на те, що ГА засновані на генетику, то і більша частина термінології відповідає їй. Будь генетичний алгоритм працює на основі початкової інформації. Безліч початкових значень є популяція Пt = {п1, п2, …, пп}, де пі = {п1, …, гv}. Розберемо докладніше:
- t – номер ітерації. t1, …, tk – означає ітерації алгоритму з 1 по k, і на кожній ітерації створюється нова популяція рішень.
- n – розмір популяції Пt.
- п1, …, пі – хромосома, особина, або організм. Хромосома або ланцюжок – це закодована послідовність генів, кожен з яких має порядковий номер. При цьому слід мати на увазі, що хромосома може бути приватним випадком особини (організму).
- гv – це гени, що є частиною закодованого рішення.
- Локус – це порядковий номер гена в хромосомі. Алель – значення гена, який може бути як цілим, так і функціональним.
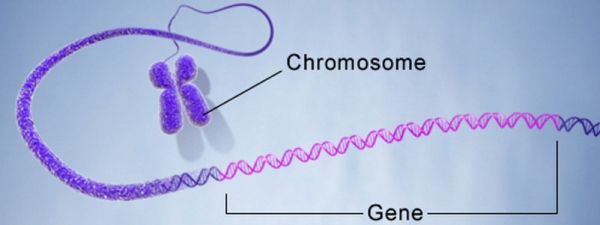
Що значить “закодований” в контексті ГА? Зазвичай будь-яке значення кодується на основі будь-якого алфавіту. Найпростішим прикладом є переклад чисел з десятеричной системі числення у двійкове подання. Таким чином алфавіт представляється як множина {0, 1}, а число 15710 буде кодуватися хромосомою 100111012 , що складається з восьми генів.
Батьки і нащадки
Батьками називаються елементи, які визначаються у відповідності з заданим умовою. Наприклад, часто такою умовою є випадковість. Вибрані елементи за рахунок операцій схрещування і мутації породжують нові, які називаються нащадками. Таким чином, батьки протягом реалізації однієї ітерації генетичного алгоритму створюють нове покоління.
Нарешті, еволюцією в даному контексті буде чергування поколінь, кожне нове з яких відрізняється набором хромосом в догоду кращої пристосованості, тобто більш придатного відповідності заданим умовам. Загальний генетичний фон в процесі еволюції називається генотипом, а формування зв’язку організму з зовнішнім середовищем – фенотипом.
Функція пристосованості
Чари генетичного алгоритму функції придатності. У кожної особини є своє значення, яке можна дізнатися через функцію пристосування. Її головним завданням є оцінка цих значень у різних альтернативних рішень і вибір найкращого з них. Іншими словами, найбільш пристосованого.
В оптимізаційних задачах функція пристосованості носить назву цільової, в теорії управління називається похибкою, теорії ігор – функцією вартості, і т. д. Що саме буде представлено у вигляді функції пристосування, залежить від розв’язуваної задачі.
У кінцевому підсумку можна зробити висновок, що генетичні алгоритми аналізують популяцію особин, організмів або хромосом, кожна з яких представлена комбінацією генів (безліччю деяких значень), і виконують пошук оптимального рішення, перетворюючи особини популяції допомогою проведення штучної еволюції серед них.
Відхилення в ту або іншу сторону окремих елементів у загальному випадку знаходяться у відповідності з нормальним законом розподілу величин. При цьому ГА забезпечує спадковість ознак, найбільш пристосовані з яких закріплюються, забезпечуючи тим самим кращу популяцію.
Базовий генетичний алгоритм
Розкладемо по кроках найбільш простий (класичний) ГА.
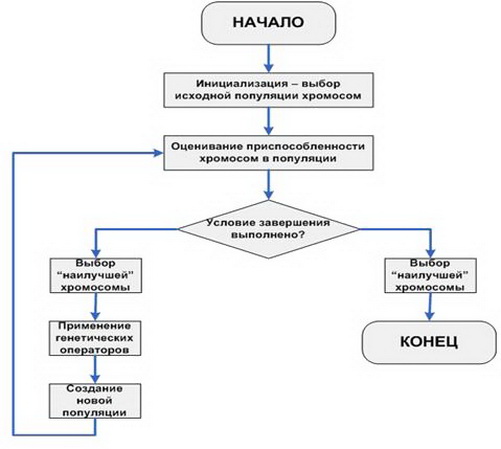
Коротко пройдемося по мало очевидним частин алгоритму. Умов припинення роботи може бути два:
Генетичними операторами є оператор мутацій і оператор схрещування. Мутація змінює випадкові гени з певною ймовірністю. Як правило, ймовірність мутації має низьке числове значення. Поговоримо детальніше про процедуру генетичного алгоритму “схрещування”. Він відбувається за наступним принципом:
Тривіальний приклад
Вирішимо завдання генетичним алгоритмом на прикладі пошуку особини з максимальним числом одиниць. Нехай особина складається з 10 генів. Задамо первинну популяцію в кількості восьми особин. Очевидно, найкращою особиною повинна бути 1111111111. Складемо для вирішення ГА.
- Ініціалізація. Виберемо 8 випадкових особин:
| п1 | 1110010101 | п5 | 0101000110 |
| п2 | 1100111010 | п6 | 0100110101 |
| п3 | 1110011110 | п7 | 0110111011 |
| п4 | 1011000000 | п8 | 0100001001 |
- Оцінка пристосованості. Очевидно, в нашому генетичному алгоритмі функція придатності F буде підраховувати кількість одиниць у кожної особини. Таким чином, маємо:
| пі | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| F(пі) | 6 | 7 | 8 | 3 | 4 | 5 | 7 | 3 |
З таблиці видно, що особини 3 і 7 мають найбільше число одиниць, а отже є найбільш придатними членами популяції для вирішення завдання. Так як на даний момент рішення необхідного якості немає, алгоритм продовжує роботу. Необхідно провести селекцію особин. Для простоти пояснення нехай селекція відбувається випадковим чином, і ми отримуємо вибірку особин {п7, п3, п1, п7, п3, п7, п4, п2} – це батьки для нової популяції.
- Використання генетичних операторів. Знову для простоти припустимо, що ймовірність мутацій дорівнює 0. Іншими словами всі 8 особин передають свої гени такими, які є. Для проведення схрещування, складемо пари особин випадковим чином: (п2, п7), (п1, п7), (п3, п4) і (п3, п7). Так само випадковим чином вибираються точки схрещування для кожної пари:
| Пара | (п2, п7) | (п1, п7) | (п3, п4) | (п3, п7) |
| Батьки |
[1100111010] [0110111011] |
[1110010101] [0110111011] |
[1110011110] [1011000000] |
[1110011110] [0110111011] |
| Тскі |
3 |
5 | 2 | 8 |
| Нащадки |
[1100111011] [0110111010] |
[1110011011] [0110110101] |
[1111000000] [1010011110] |
[1110011111] [0110111010] |
- Складання нової популяції, що складається з нащадків:
| п1 | 1100111011 | п5 | 1111000000 |
| п2 | 0110111010 | п6 | 1010011110 |
| п3 | 1110011011 | п7 | 1110011111 |
| п4 | 0110110101 | п8 | 0110111010 |
- Оцінюємо пристосованість кожної особини нової популяції:
| пі | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| F(пі) | 7 | 6 | 7 | 6 | 4 | 6 | 8 | 6 |
Подальші дії очевидні. Найцікавіше в ГА відкривається у випадку, якщо оцінити середня кількість одиниць в кожній популяції. У першій популяції в середньому на кожну особину доводилося 5,375 одиниць, в популяції нащадків – 6,25 одиниць на особину. І така особливість буде спостерігатися навіть у випадку, якщо в ході мутацій і схрещування особина з найбільшим числом одиниць в першій популяції загубиться.
План реалізації
Створення генетичного алгоритму являє собою достатньо складну задачу. Спочатку перерахуємо план у вигляді кроків, після чого докладніше розберемо кожний з них.
Перший етап свідчить про те, що алфавіт, в який будуть кодуватися всі елементи множини рішень або популяції, повинен бути досить гнучким, щоб одночасно дозволяв виробляти потрібні операції випадкових перестановок і оцінювати пристосованість елементів, як первинних, так і пройшли через зміни. Математично встановлено, що створити ідеальний алфавіт для цих цілей неможливо, тому його складання – це один з найбільш складних і відповідальних етапів, щоб забезпечити стабільну роботу ГА.

Не менш складним є визначення операторів зміни і створення нащадків. Існує безліч операторів, які здатні виконувати необхідні дії. Наприклад, з біології відомо, що кожен вид може розмножуватися двома способами: статевим (схрещування) і безстатевим (мутаціями). В першому випадку батьки обмінюються генетичним матеріалом, у другому – відбуваються мутації, визначені внутрішніми механізмами організму і зовнішнім впливом. Крім цього, можна застосовувати неіснуючі в живій природі моделі розмноження. Наприклад, використовувати гени трьох і більше батьків. Аналогічно схрещування в генетичному алгоритмі мутації може бути закладений різноманітний механізм.
Вибір способу виживання може бути дуже оманливим. Існує безліч способів в генетичному алгоритмі для селекції. І, як показує практика, правило “виживання найбільш пристосованого” далеко не завжди виявляється кращим. При рішенні складних технічних проблем часто виявляється, що найкраще рішення випливає з безлічі середніх або навіть гірших. Тому найчастіше прийнято використовувати імовірнісний підхід, який свідчить, що найкраще рішення має більше шансів на виживання.

Останній етап забезпечує гнучкість роботи алгоритму, якої немає ні в якого іншого. Первинну популяцію рішень можна задати як виходячи з яких-небудь відомих даних, так і абсолютно випадковим чином простою перестановкою генів усередині особин і створенням випадкових особин. Однак завжди варто пам’ятати, що від початкової популяції багато в чому залежить ефективність алгоритму.
Ефективність
Ефективність генетичного алгоритму повністю залежить від правильності реалізації етапів, описаних в плані. Особливо впливовим пунктом тут є створення первинної популяції. Для цього існує безліч підходів. Опишемо декілька:

Таким чином, можна зробити висновок, що ефективність генетичних алгоритмів в чому залежить від досвіду програміста в цьому питанні. Це є недоліком генетичних алгоритмів, так і їх перевагою.











