Закон Ома був вперше сформульовано німецьким фізиком і математиком Георгом Симоном Омом. Закон Ома є основним законом для електричних ланцюгів з постійним струмом. Він встановлює зв’язок між напругою або падінням потенціалу, силою струму і опором ланцюга. Розглянемо детальніше закон Ома та інші основні закони постійного струму.
Історична довідка

Георг Симон Ом народився в місті Ерлангені (Німеччина) 16 березня 1789 року у протестантській родині. З раннього дитинства він почав працювати в слюсарній майстерні свого батька. Кар’єра фізика почалася у Ома в Політехнічному університеті Нюрнберга. До кінця своїх днів він викладав фізику в університеті Мюнхена.
Головною заслугою Ома у фізиці є те, що він ввів і описав таку фізичну величину, як електричний опір. Він вперше сформулював у математичному вигляді взаємозв’язок між різницею потенціалів, силою струму та електричним опором ланцюга, за що одиниця опору була названа на його прізвища.
Нові ідеї Ома не одразу прийняло світове наукове співтовариство, лише в 1841 році Королівське Товариство в Лондоні нагородило Ома медаллю Коплі, а Мюнхенський університет в 1849 році виділив йому кафедру фізики.
Ом протягом своєї наукової діяльності займався не тільки електричними ланцюгами. У 1840 році він вивчав звукові хвилі, а з 1852 року займався оптикою, зокрема, феноменом інтерференції. Помер вчений у Мюнхені 6 липня 1854 року.
Експерименти Ома
Перед тим як Ом виклав свій знаменитий закон для постійного струму, інші вчені провели безліч експериментів з електричними ланцюгами. Слід зазначити експерименти британця Генрі Кавендіша, який досліджував поведінку банок Лейдена в 1781 році, але так і не зміг опублікувати свої висновки.
В даний час фізики розташовують інструментами, які дозволяють з необхідною точністю виміряти будь-які параметри електричного кола, в кінці XVIII-початку XIX століття таких приладів не було, що створювало труднощі для відкриття Омом закону для постійного струму.
Саме тому Ом вирішив самостійно виготовити такий прилад. Зокрема, він використовував крутильні ваги Кулона, але удосконалив їх, додавши до них магнітний елемент. При цьому вчений використовував відкриття Гансом Християном Эрстедом в 1819 році того факту, що провідник зі струмом робить силову дію на намагнічену голку, що знаходиться поблизу від нього. Використовуючи свої нові крутильні ваги, провідні кабелі різної довжини, джерело електричного струму і посудини із ртуттю, Ом зміг виміряти зменшення сили, з якою провідник зі струмом діє на голку при збільшенні довжини цього провідника.
В результаті цих експериментів вчений отримав наступну математичну залежність: V = 0,41 lg (1+x), де V – напруга в ланцюзі, x – довжина провідника з струмом. Це вираз згодом призвело вченого до формулювання закону постійного струму.
Поняття про силу електричного струму
Перш ніж розглядати закон Ома для постійного струму, введемо поняття сили струму. Деякі частинки в природі володіють так званим електричним зарядом. Поняття сили струму безпосередньо пов’язане з переміщенням цих заряджених частинок, які в більшості випадків є або іонами, або електронами. Під силою струму в фізиці розуміють кількість заряду, що проходить через переріз провідника за одиницю часу, що математично виражається у вигляді наступного виразу: I = dq/dt.
Одиницею сили струму в СІ є ампер (А), 1 А – це така сила струму, при якій через провідника за 1 с переноситься заряд у 1 Кл. Оскільки позитивні і негативні заряди рухаються в протилежних напрямках в одному і тому ж електричному полі, то силу струму прийнято визначати за напрямом руху позитивних зарядів.
Швидкість руху заряджених частинок в електричному полі

У фізиці закон постійного струму формулюється для I=const, а це означає, що кожна частинка-носій електричного заряду повинна рухатися з постійною швидкістю. Проте, щоб існував електричний струм, необхідно наявність заряджених частинок, здатних рухатися, а також існування електричного поля. Останнє діє на електричний заряд q з певною силою. Ця сила визначається за формулою: F = q*E, тут E – напруженість електричного поля.
Згідно другого закону Ньютона, заряджена частинка набуває прискорення a = q*E/m, де m – маса частинки. Оскільки всі величини в цьому виразі є постійними, то і прискорення також буде незмінним і відмінним від нуля. Всі ці міркування справедливі для випадку руху заряду в порожньому просторі, якщо ж він рухається в будь-якому середовищі, то з боку середовища виникає деякий опір.
Наприклад, що рухається під дією електричної сили в металевому провіднику електрон відчуває постійні зіткнення з іонами, що утворюють кристалічну решітку металеву. Ці зіткнення призводять до того, що електрон починає рухатися з постійною швидкістю, яка називається швидкістю дрейфу. Саме у взаємодії електрона з іонами решітки полягає природа електричного опору.
Рух електрона в металевому провіднику можна порівняти з рухом краплі дощу в повітрі, оскільки ця крапля не падає з прискоренням вільного падіння, а здійснює рівномірний рух з-за впливу сили опору з боку повітря.
Локальний закон Ома
У кожній школі починають вивчати в 8 класі закони постійного струму. При цьому формулюють закон Ома спочатку в локальній формі. Щоб це зробити, візьмемо для прикладу металевий провідник.
У металі валентні електрони, тобто електрони, що знаходяться на зовнішніх енергетичних оболонках атомів, слабо пов’язані з атомними ядрами, тому в об’ємному матеріалі вони не належать конкретній атомному ядру, а є вільними або усуспільненими. Кожен такий електрон при кімнатній температурі хаотично рухається в металевому кристалі. Це рух подібно руху молекули в газі. Швидкість теплового руху електрона велика, вона становить близько 106 м/с. Оскільки рух є равновероятным у всіх напрямках, то воно не призводить до виникнення електричного струму.
Струм з’являється, якщо цей провідник помістити в електричне поле. В результаті цього електрон набуває дрейфовую швидкість, порядок величини якої становить 10-6 м/с. В результаті сила електричного струму через площу перерізу A запишеться у вигляді наступної формули: I = n*q2*E*t*A/me, тут n – кількість електронів, які проходять через майданчик A за час t, що є часом між двома зіткненнями електрона з іонами решітки, me – маса електрона.
Отриманий вираз можна переписати у вигляді J = I/A = σ*E, де J – щільність електричного струму, σ – властивість матеріалу, яка називається електричною провідністю. Це вираз для густини струму носить назву закону Ома для постійного струму в локальній формі.
Закон Ома в макроскопічної формі

В школі у 8 класі закон постійного струму також розглядається в макроскопічної формі. Його легко можна отримати з відповідного закону в локальній формі. Для цього необхідно визначити напругу або падіння потенціалу в електричної ланцюга у вигляді наступного виразу: ΔV = E*l, де l – довжина провідника з струмом, а ΔV – напругу на його кінцях.
В результаті закон Ома прийме вигляд: ΔV = I*l/(σ*A) = R*I, де R – електричний опір. Як видно з закону постійного електричного струму в макроскопічної форми, величина R є зворотною величиною електричної провідності σ, тобто чим краще матеріал проводить струм, тим менше його електричний опір. Також важливо помітити, що в той час як σ є властивістю матеріалу, з якого зроблений провідник, R є властивістю конкретного провідника, і залежить не тільки від матеріалу, але і від його геометричних параметрів (довжини і площі перерізу).
Застосовність і важливість класичного закону Ома
Закон Ома в класичній або макроскопічної формі записується у вигляді: V = I*R. Для металів R є постійною величиною, незалежно від сили струму, що проходить через провідник. Однак, в деяких матеріалах, наприклад, у напівпровідниках, це не так. Матеріали, в яких електричне опір є постійною величиною, називаються лінійними або омічними. Для них вольт-амперна характеристика, тобто функція залежності напруги від сили струму U(I) є лінійною.
Закон Ома не може вважатися фундаментальним законом природи, оскільки він справедливий тільки для певного класу матеріалів, головним чином, це метали. Однак, він відіграє важливу роль у фізиці і в повсякденному житті, оскільки дозволяє простим способом визначити важливі фізичні величини в електричної ланцюга. Зокрема, завдяки закону Ома для кола постійного струму обчислюють втрати електроенергії при її передачі і споживанні. Закон Ома також використовують для обчислення необхідного значення опору, яке варто включити в електричний ланцюг, щоб вона виконувала свої функції з максимальним ККД.
Залежність питомого опору від температури для омічних матеріалів
Розглядаючи закони ланцюгів постійного струму, слід згадати про те, як змінюється опір з підвищенням температури. За аналогією з електричною провідністю матеріалу у фізиці вводять поняття питомого електричного опору ρ, воно пов’язане з опором наступною формулою: R = l*ρ/A.
Емпіричним шляхом встановлено, що для омічних матеріалів ρ підпорядковується наступній залежності від температури: ρ = ρ0*[1+α(T-T0)+β(T-T0)2+…], тут ρ0 – питомий опір матеріалу при температурі T0, яку часто вважають рівною 20°C.
Для металевих матеріалів в інтервалі від 0 до 200 °С питомий опір лінійно залежить від температури, тобто ρ = ρ0*[1+α(T-T0)], де α – коефіцієнт температурного опору, який для металів є позитивною величиною, це говорить про те, що електричний опір лінійно збільшується із зростанням температури для металів. Така поведінка пов’язано з зменшенням відстані, яку проходить електрон між двома зіткненнями з іонами решітки, при збільшенні температури.
Цікаво відзначити, що у напівпровідників питомий опір зменшується з зростанням температури. Цей факт пов’язаний зі збільшенням кількості носіїв електричного струму при нагріві напівпровідникового матеріалу, наприклад, кремнію або германію.
Закони Кірхгофа

У школах в 10 класі закони постійного струму не обмежуються лише законом Ома. За шкільною програмою також вивчають закони Кірхгофа. Існують два закони Кірхгофа для постійного струму. Засновані вони на законі збереження енергії і заряду в електричному ланцюзі. Нижче наведені формулювання для обох законів Кірхгофа:
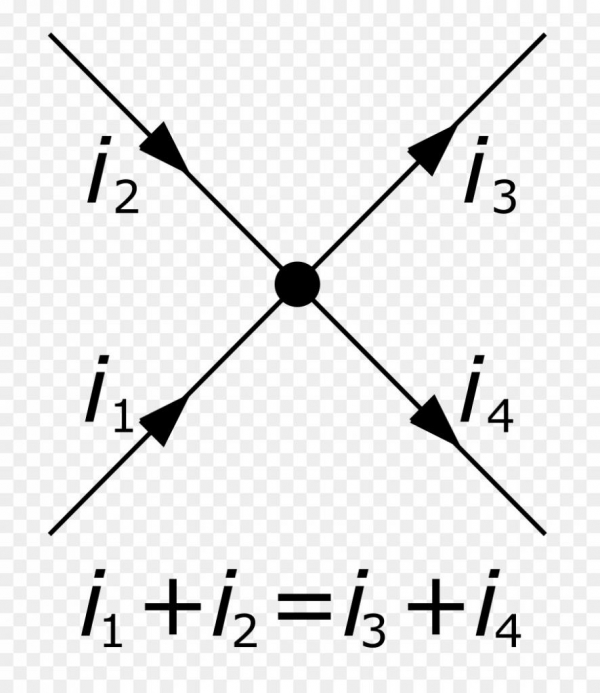
Записані вперше ці закони були в 1846 році. В даний час вони широко використовуються в електричній техніці та електроніці для визначення невідомих струмів, напруг і опорів у колах. Зазначимо, що у разі наявності ненульового електричного опору в ланцюзі R, частина електричної енергії перетвориться в тепло Q, яке називається джоулевским і обчислюється за формулою Q = I2Rt, де t – час протікання струму по елементу ланцюга з опором R.
Практичне застосування законів Ома і Кірхгофа
Наведемо приклад завдання на закони постійного струму. На малюнку нижче наведений приклад електричної ланцюга, що складається з двох контурів, двох джерел напруги і 5 резисторів з різним опором. Завдання полягає в знаходженні невідомих струмів Ix і Iy. Відразу слід сказати, що напрям в обох контурах вибрано довільно, в даному випадку за годинниковою стрілкою.
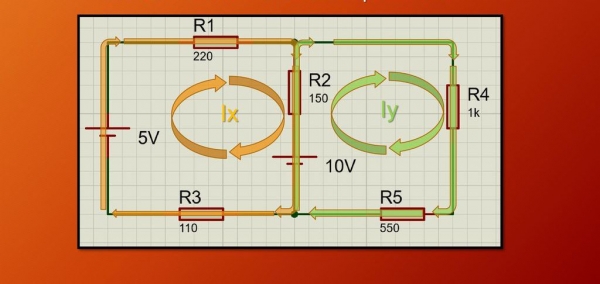
Далі необхідно розглянути кожен контур окремо. Для початку звернемо увагу на контур з невідомим струмом Ix. Для вибраного контуру необхідно застосувати другий закон Кірхгофа, то є закон, який говорить про рівність падінь напруги на всіх резисторах і напруги живлення від усіх джерел струму. Застосовуючи цей закон, отримуємо: 5-10 = Ix*R1+(Ix-Iy)*R2+Ix*R3. При складанні цього виразу враховувався знак обраного напрямку сили струму Ix, як позитивного спрямування, тому різниця потенціалів на джерелі в 5 є позитивною, а на джерелі в 10 – негативною. Також відзначимо, що, розглядаючи даний контур, також необхідно враховувати струм Iy, який тече згідно з введеними позначеннями через резистор R2.
Тепер отримаємо аналогічне рівняння для другого контуру з невідомим струмом Iy. Це вираз буде мати вигляд: 10 = (Iv-Ix)*R2+Iy*R4+Iy*R5. У другому контурі існує тільки одне джерело живлення (10), тому тільки він входить в отримане з 2-го закону Кірхгофа вираз.
Таким чином, отримано два рівняння, в яких є дві невідомих: Ix і Iy. Залишилося об’єднати ці вирази у систему лінійних рівнянь, і вирішити її. Наведений нижче малюнок показує розглядається електричну ланцюг і отриману систему рівнянь для визначення невідомих струмів.
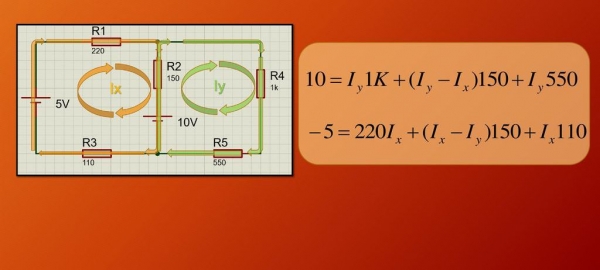
Вирішуючи систему рівнянь, отримуємо, що Ix = -0,00882 А = -8,82 мА, а Iy = 0,0051 А = 5,1 мА. Знак “мінус” свідчить про те, що в дійсності струм тече в напрямку, який протилежний вибраному. У підсумку через резистори R1, R3 тече струм 8,82 мА, через резистори R4, R5 – 5,1 мА, а через резистор R2 – Iy-Ix = 13,92 мА.