Є проблеми з елементарною геометрією? Ця стаття допоможе вам вирішити одну з них. Тут ви дізнаєтеся про те, що таке площа в математиці, про одиниці її виміру та інших важливих аспектах цієї теми. Розбір деяких конкретних прикладів дасть вам можливість глибше вивчити питання.
Що таке площа в математиці?
Площа – це міра того, скільки простору є на плоскій поверхні. Наприклад, є два однакових шматка паперу, чия сумарна площа, очевидно, більше ніж кожного з них окремо.
Площі фігур у математики обчислюються різними шляхами, залежно від їх форми. Наприклад, у випадку з прямокутником необхідно знайти добуток його висоти і ширини. Подивимося на малюнок.
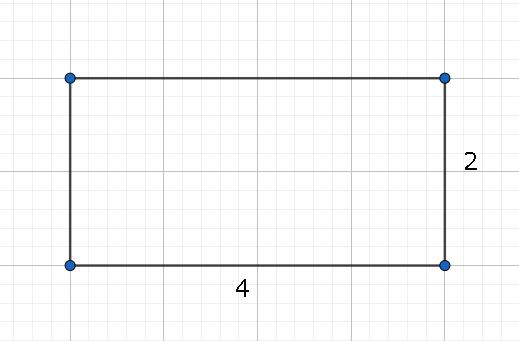
Маємо відповідь: 2 × 4 = 8 см2. Задача вирішена.
Перевірити його можна вручну підрахувавши кількість великих квадратиків всередині прямокутника. Подібної задачі достатньо для того, щоб пояснити, що таке площа в математиці. Але в цій темі є ще й інші важливі нюанси.
Одиниця виміру площі в математиці
Вимірюється площа в квадратних одиницях. Тобто її можна визначити як деяку кількість чотирикутників, чиї сторони дорівнюють 1. При цьому, якщо поміняти місцями значення довжини і висоти, кінцевий результат не зміниться.
Примітка! Всі величини мають бути в однакових одиницях виміру.
Припустимо, що дані задані в сантиметрах. Як тоді правильно визначити це на папері?
Замість того щоб писати “вісім квадратних сантиметрів”, можна використовувати запис виду “8 см2”. Досить просто звести скорочену форму заходи у другу ступінь.











