Таке поняття, як матриця, використовується і виникає розділи вищої математики. Найчастіше вона зустрічається у системі лінійних рівнянь. Так яке ж основне поняття матриці? Щоб зрозуміти це, не обов’язково бути математичним генієм.
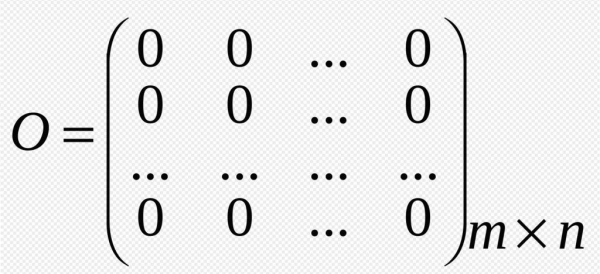
Матриця – це щось таке, що представляє із себе систему з чисел mn, які в математиці записуються у вигляді таблиць, в яких m – це рядки, а n – стовпці. На її перетині знаходяться елементи. Розмір матриці залежить від кількості рядків і стовпців.
Спочатку розглядалася матриця трикутної форми, але вона не зручна для вирішення складних рівнянь, тому в математиці використовують прямокутний аналог. Така система вважається зручною для вирішення поставленого завдання.
Звідки прийшла матриця
Якщо говорити про першому згадуванні, то поняття про матриці прийшов з Китаю, а точніше воно було пов’язане з «магічними квадратами». Ці таблиці вважалися оберегами за рахунок написаних на них чисел. У той час не було ні самого поняття матриці, ні способів її рішення. Вона визначала в деяких племенах ступінь споріднення для того, щоб люди дізнавалися, вони можуть одружитися чи ні.
А ось саме поняття було введено на початку 19 століття Джеймсом Сильвестром, який був англійським математиком. Над теорією матриць працювали різні учені, створюючи комплекс рішень складних алгебраїчних задач.
Матриця і її основні види
Отже, раніше було розглянуто поняття матриці. Види матриць представлені нижче:
- Рядкова. Вона складається з одного рядка, тобто у цього виду матриці число рядків рівне m=1, а ось кількість її стовпців довільне.
- Столбцовая. Ця різновид складається всього з одного стовпця, але також може містити в собі кілька рядків. Для такого виду матриці є своя універсальна запис. Вона вказує на те, що елементи, які знаходяться в дужках, повинні бути записані у вигляді стовпця. До всього іншого, це економить не тільки місце, але і час.
- Нуль-матриця. Такий вид існує, коли всі її елементи дорівнюють 0. Позначають цю різновид матриці “Про” Свою назву цей елемент також отримав за рахунок того, що в обчисленні у неї схожі функції з нулем в теорії чисел.
- Квадратна. Цей вид матриці є найпоширенішим, його відмінність полягає в тому, що в ній рівну кількість стовпців і рядків. При з’єднанні двох елементів, що знаходяться в різних кінцях стовпця, ми отримуємо головну діагональ. У зв’язку з цим діагональна таблиця поділяється ще на кілька систем:
а) Діагональна. Цей тип квадратної матриці, в яку увійшли елементи, що належать головній діагоналі.
б) Одинична. У такого типу діагональ складається всього з однієї одиниці. При всьому цьому кожна така матриця є скалярною.
в) Скалярна. Це тип, де головна діагональ складається з одного і того ж числа.
г) Стрілкова. Це вид квадратної матриці, в якій практично всі елементи дорівнюють нулю, але при цьому складові, що входять до складу першого стовпця, а також відносять до діагоналі і першому рядку, не дорівнюють йому.
- Бінарна. Цей вид таблиці складається з нулів та одиниць.
- Матриця Паскаля – в цьому вигляді матриці всі елементи складаються з чисел, що належать до однойменного трикутника.
- Трехдиагональная. У цьому вигляді матриці ненульові елементи розташовані на трьох діагоналях, до яких належить головна з них та ті, що зверху і знизу.
Ранг матриці
Дізнавшись, що вона має різні види, потрібно сказати про таке поняття: ранг матриці. Під цим розуміють кількість незалежних лінійних стовпців або ж кількість незалежних лінійних рядків. Також ранг будь матриці – це порядок мінорів, який є найвищим, його визначник відмінний від нуля.
Позначається ранг за допомогою rang A, але зустрічається і rank A. Обидва поняття вважаються правильними, так що при різному написанні це не буде вважатися помилкою. Головне не забути про те, що ранг рядків завжди дорівнює рангу стовпців.
Дії над матрицею
Матриця є універсальною системою для вирішення алгебраїчних завдань, над нею виробляють різні дії. У їх число входить множення двох матриць, додавання, множення її на кількість і на інші матриці.
Проводячи численні дії в алгебрі, система різних матриць допомагає знайти більш легкий спосіб вирішення поставлених завдань. Це забирає менше часу і допомагає не заплутатися у великій кількості дій.
Операції, пов’язані з матрицею, що використовуються не тільки в математиці, але також і у фізиці і хімії.
